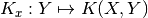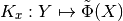Module kernels¶

operalib.kernels implements some Operator-Valued Kernel models.

class operalib.kernels.DecomposableKernel(A, scalar_kernel=<function rbf_kernel>, scalar_kernel_params=None)[source]¶

Decomposable Operator-Valued Kernel of the form:

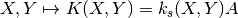
$X, Y \mapsto K(X, Y) = k_s(X, Y) A$

where A is a symmetric positive semidefinite operator acting on the outputs.

See also

DecomposableKernelMap: Decomposable Kernel map

Examples

>>> import operalib as ovk
>>> import numpy as np
>>> X = np.random.randn(100, 10)
>>> K = ovk.DecomposableKernel(np.eye(2))
>>> # The kernel matrix as a linear operator
>>> K(X, X)  
<200x200 _CustomLinearOperator with dtype=float64>

Attributes:	A : {array, LinearOperator}, shape = [n_targets, n_targets] Linear operator acting on the outputs scalar_kernel : {callable} Callable which associate to the training points X the Gram matrix. scalar_kernel_params : {mapping of string to any} Additional parameters (keyword arguments) for kernel function passed as callable object.

Methods

`__call__`(X[, Y])	Return the kernel map associated with the data X.
`get_kernel_map`(X)	Return the kernel map associated with the data X.
`get_orff_map`(X[, D, eps, random_state])	Return the Random Fourier Feature map associated with the data X.

__call__(X, Y=None)[source]¶

Return the kernel map associated with the data X.

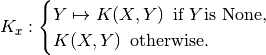
$K_x: \begin{cases} Y \mapsto K(X, Y) \enskip\text{if } Y \text{is None,} \\ K(X, Y) \enskip\text{otherwise.} \end{cases}$

Parameters:	X : {array-like, sparse matrix}, shape = [n_samples1, n_features] Samples. Y : {array-like, sparse matrix}, shape = [n_samples2, n_features], default = None Samples.
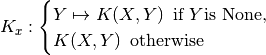
Returns:	K_x : DecomposableKernelMap, callable or LinearOperator $K_x: \begin{cases} Y \mapsto K(X, Y) \enskip\text{if } Y \text{is None,} \\ K(X, Y) \enskip\text{otherwise} \end{cases}$

__init__(A, scalar_kernel=<function rbf_kernel>, scalar_kernel_params=None)[source]¶

Initialize the Decomposable Operator-Valued Kernel.

Parameters:	A : {array, LinearOperator}, shape = [n_targets, n_targets] Linear operator acting on the outputs scalar_kernel : {callable} Callable which associate to the training points X the Gram matrix. scalar_kernel_params : {mapping of string to any}, optional Additional parameters (keyword arguments) for kernel function passed as callable object.

__weakref__¶: list of weak references to the object (if defined)

get_kernel_map(X)[source]¶

Return the kernel map associated with the data X.

$K_x: Y \mapsto K(X, Y)$

Parameters:	X : {array-like, sparse matrix}, shape = [n_samples, n_features] Samples.
Returns:	K_x : DecomposableKernelMap, callable .. math:: K_x: Y mapsto K(X, Y).

get_orff_map(X, D=100, eps=1e-05, random_state=0)[source]¶

Return the Random Fourier Feature map associated with the data X.

$K_x: Y \mapsto \tilde{\Phi}(X)$

Parameters:	X : {array-like, sparse matrix}, shape = [n_samples, n_features] Samples.
Returns:	tilde{Phi}(X) : Linear Operator, callable

class operalib.kernels.DotProductKernel(mu, p)[source]¶

Dot product Operator-Valued Kernel of the form:

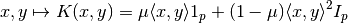
$x, y \mapsto K(x, y) = \mu \langle x, y \rangle 1_p + (1-\mu) \langle x, y \rangle^2 I_p$

See also

DotProductKernelMap: Dot Product Kernel Map

Examples

>>> import operalib as ovk
>>> import numpy as np
>>> X = np.random.randn(100, 10)
>>> K = ovk.DotProductKernel(mu=.2, p=5)
>>> # The kernel matrix as a linear operator
>>> K(X, X)  
<500x500 _CustomLinearOperator with dtype=float64>

Attributes:	mu : {array, LinearOperator}, shape = [n_targets, n_targets] Tradeoff between shared and independant components p : {Int} dimension of the targets (n_targets).

Methods

`__call__`(X[, Y])	Return the kernel map associated with the data X.
`get_kernel_map`(X)	Return the kernel map associated with the data X.

__call__(X, Y=None)[source]¶

Return the kernel map associated with the data X.

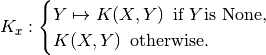
$K_x: \begin{cases} Y \mapsto K(X, Y) \enskip\text{if } Y \text{is None,} \\ K(X, Y) \enskip\text{otherwise.} \end{cases}$

Parameters:	X : {array-like, sparse matrix}, shape = [n_samples1, n_features] Samples. Y : {array-like, sparse matrix}, shape = [n_samples2, n_features], default = None Samples.
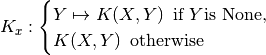
Returns:	K_x : DotProductKernelMap, callable or LinearOperator $K_x: \begin{cases} Y \mapsto K(X, Y) \enskip\text{if } Y \text{is None,} \\ K(X, Y) \enskip\text{otherwise} \end{cases}$

__init__(mu, p)[source]¶

Initialize the Dot product Operator-Valued Kernel.

Parameters:	mu : {float} Tradeoff between shared and independant components. p : {integer} dimension of the targets (n_targets).

__weakref__¶: list of weak references to the object (if defined)

get_kernel_map(X)[source]¶

Return the kernel map associated with the data X.

$K_x: Y \mapsto K(X, Y)$

Parameters:	X : {array-like, sparse matrix}, shape = [n_samples, n_features] Samples.
Returns:	K_x : DotProductKernelMap, callable .. math:: K_x: Y mapsto K(X, Y).

class operalib.kernels.RBFCurlFreeKernel(gamma)[source]¶

Curl-free Operator-Valued Kernel of the form:

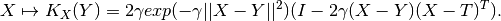
$X \mapsto K_X(Y) = 2 \gamma exp(-\gamma||X - Y||^2)(I - 2\gamma(X - Y) (X - T)^T).$

See also

RBFCurlFreeKernelMap: Curl-free Kernel map

Examples

>>> import operalib as ovk
>>> import numpy as np
>>> X = np.random.randn(100, 2)
>>> K = ovk.RBFCurlFreeKernel(1.)
>>> # The kernel matrix as a linear operator
>>> K(X, X)  
<200x200 _CustomLinearOperator with dtype=float64>

Attributes:	gamma : {float} RBF kernel parameter.

Methods

`__call__`(X[, Y])	Return the kernel map associated with the data X.
`get_kernel_map`(X)	Return the kernel map associated with the data X.
`get_orff_map`(X[, D, random_state])	Return the Random Fourier Feature map associated with the data X.

__call__(X, Y=None)[source]¶

Return the kernel map associated with the data X.

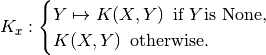
$K_x: \begin{cases} Y \mapsto K(X, Y) \enskip\text{if } Y \text{is None,} \\ K(X, Y) \enskip\text{otherwise.} \end{cases}$

Parameters:	X : {array-like, sparse matrix}, shape = [n_samples1, n_features] Samples. Y : {array-like, sparse matrix}, shape = [n_samples2, n_features], default = None Samples.
Returns:	K_x : DecomposableKernelMap, callable or LinearOperator .. math:: K_x: begin{cases} Y mapsto K(X, Y) enskiptext{if } Y text{is None,} \ K(X, Y) enskiptext{otherwise} end{cases}

__init__(gamma)[source]¶

Initialize the Decomposable Operator-Valued Kernel.

Parameters:	gamma : {float}, shape = [n_targets, n_targets] RBF kernel parameter.

__weakref__¶: list of weak references to the object (if defined)

get_kernel_map(X)[source]¶

Return the kernel map associated with the data X.

$K_x: Y \mapsto K(X, Y)$

Parameters:	X : {array-like, sparse matrix}, shape = [n_samples, n_features] Samples.
Returns:	K_x : DecomposableKernelMap, callable .. math:: K_x: Y mapsto K(X, Y).

get_orff_map(X, D=100, random_state=0)[source]¶

Return the Random Fourier Feature map associated with the data X.

$K_x: Y \mapsto \tilde{\Phi}(X)$

Parameters:	X : {array-like, sparse matrix}, shape = [n_samples, n_features] Samples.
Returns:	tilde{Phi}(X) : Linear Operator, callable

class operalib.kernels.RBFDivFreeKernel(gamma)[source]¶

Divergence-free Operator-Valued Kernel of the form:

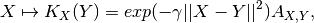
$X \mapsto K_X(Y) = exp(-\gamma||X-Y||^2)A_{X,Y},$

where,

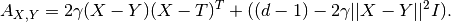
$A_{X,Y} = 2\gamma(X-Y)(X-T)^T+((d-1)-2\gamma||X-Y||^2 I).$

See also

RBFDivFreeKernelMap: Divergence-free Kernel map

Examples

>>> import operalib as ovk
>>> import numpy as np
>>> X = np.random.randn(100, 2)
>>> K = ovk.RBFDivFreeKernel(1.)
>>> # The kernel matrix as a linear operator
>>> K(X, X)  
<200x200 _CustomLinearOperator with dtype=float64>

Attributes:	gamma : {float} RBF kernel parameter.

Methods

`__call__`(X[, Y])	Return the kernel map associated with the data X.
`get_kernel_map`(X)	Return the kernel map associated with the data X.
`get_orff_map`(X[, D, random_state])	Return the Random Fourier Feature map associated with the data X.

__call__(X, Y=None)[source]¶

Return the kernel map associated with the data X.

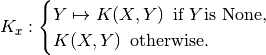
$K_x: \begin{cases} Y \mapsto K(X, Y) \enskip\text{if } Y \text{is None,} \\ K(X, Y) \enskip\text{otherwise.} \end{cases}$

Parameters:	X : {array-like, sparse matrix}, shape = [n_samples1, n_features] Samples. Y : {array-like, sparse matrix}, shape = [n_samples2, n_features], default = None Samples.
Returns:	K_x : DecomposableKernelMap, callable or LinearOperator .. math:: K_x: begin{cases} Y mapsto K(X, Y) enskiptext{if } Y text{is None,} \ K(X, Y) enskiptext{otherwise} end{cases}

__init__(gamma)[source]¶

Initialize the Decomposable Operator-Valued Kernel.

Parameters:	gamma : {float}, shape = [n_targets, n_targets] RBF kernel parameter.

__weakref__¶: list of weak references to the object (if defined)

get_kernel_map(X)[source]¶

Return the kernel map associated with the data X.

$K_x: Y \mapsto K(X, Y)$

Parameters:	X : {array-like, sparse matrix}, shape = [n_samples, n_features] Samples.
Returns:	K_x : DecomposableKernelMap, callable .. math:: K_x: Y mapsto K(X, Y).

get_orff_map(X, D=100, random_state=0)[source]¶

Return the Random Fourier Feature map associated with the data X.

$K_x: Y \mapsto \tilde{\Phi}(X)$

Parameters:	X : {array-like, sparse matrix}, shape = [n_samples, n_features] Samples.
Returns:	tilde{Phi}(X) : Linear Operator, callable

operalib.kernel_maps implement some Operator-Valued Kernel maps associated to the operator-valued kernel models defined in operalib.kernels.

class operalib.kernel_maps.DecomposableKernelMap(X, A, scalar_kernel, scalar_kernel_params)[source]¶

Decomposable Operator-Valued Kernel map of the form:

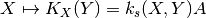
$X \mapsto K_X(Y) = k_s(X, Y) A$

where A is a symmetric positive semidefinite operator acting on the outputs. This class just fixes the support data X to the kernel. Hence it naturally inherit from DecomposableKernel.

See also

DecomposableKernel: Decomposable Kernel

Examples

>>> import operalib as ovk
>>> import numpy as np
>>> X = np.random.randn(100, 10)
>>> K = ovk.DecomposableKernel(np.eye(2))
>>> Gram = K(X, X)
>>> Gram

<200x200 _CustomLinearOperator with dtype=float64>
>>> C = np.random.randn(Gram.shape[0])
>>> Kx = K(X)  # The kernel map.
>>> np.allclose(Gram * C, Kx(X) * C)

True

Attributes:	n : {Int} Number of samples. d : {Int} Number of features. X : {array-like, sparse matrix}, shape = [n_samples, n_features] Support samples. Gs : {array-like, sparse matrix}, shape = [n, n] Gram matrix associated with the scalar kernel.

Methods

`Gram_dense`(X)	Return the dense Gram matrix associated with the data Y.
`__call__`(Y)	Return the Gram matrix associated with the data Y as a linear operator.
`get_kernel_map`(X)	Return the kernel map associated with the data X.
`get_orff_map`(X[, D, eps, random_state])	Return the Random Fourier Feature map associated with the data X.

Gram_dense(X)[source]¶

Return the dense Gram matrix associated with the data Y.

$K(X, Y)$

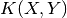
Parameters:	Y : {array-like, sparse matrix}, shape = [n_samples1, n_features] Samples.
Returns:	K(X, Y) : {array-like} Returns K(X, Y).

T¶: Transposition.

__call__(Y)[source]¶

Return the Gram matrix associated with the data Y as a linear operator.

$K(X, Y)$

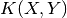
Parameters:	Y : {array-like, sparse matrix}, shape = [n_samples1, n_features] Samples.
Returns:	K(X, Y) : LinearOperator Returns K(X, Y).

__init__(X, A, scalar_kernel, scalar_kernel_params)[source]¶

Initialize the Decomposable Operator-Valued Kernel.

Parameters:

X: {array-like, sparse matrix}, shape = [n_samples1, n_features]: Support samples.
A : {array, LinearOperator}, shape = [n_targets, n_targets]: Linear operator acting on the outputs
scalar_kernel : {callable}: Callable which associate to the training points X the Gram matrix.
scalar_kernel_params : {mapping of string to any}, optional: Additional parameters (keyword arguments) for kernel function passed as callable object.

__mul__(Ky)[source]¶

Syntaxic sugar.

If Kx is a compatible decomposable kernel, returns

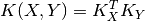
$K(X, Y) = K_X^T K_Y$

Parameters:	Ky : {DecomposableKernelMap} Compatible kernel Map (e.g. same kernel but different support data X).
Returns:	K(X, Y) : LinearOperator Returns K(X, Y).

Examples

>>> import operalib as ovk
>>> import numpy as np
>>> X = np.random.randn(100, 10)
>>> K = ovk.DecomposableKernel(np.eye(2))
>>> Gram = K(X, X)
>>> Gram

<200x200 _CustomLinearOperator with dtype=float64>
>>> C = np.random.randn(Gram.shape[0])
>>> Kx = K(X)  # The kernel map.
>>> Ky = K(X)
>>> np.allclose(Gram * C, (Kx.T * Ky) * C)

True

class operalib.kernel_maps.DotProductKernelMap(X, mu, p)[source]¶

Dot Product Operator-Valued Kernel map of the form:

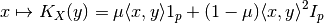
$x \mapsto K_X(y) = \mu \langle x, y \rangle 1_p + (1-\mu) \langle x, y \rangle^2 I_p$

This class just fixes the support data X to the kernel.

See also

DotProductKernel: Dot Product Kernel

Examples

>>> import operalib as ovk
>>> import numpy as np
>>> X = np.random.randn(100, 10)
>>> K = ovk.DotProductKernel(mu=0.2, p=5)
>>> Gram = K(X, X)
>>> Gram

<500x500 _CustomLinearOperator with dtype=float64>
>>> C = np.random.randn(Gram.shape[0])
>>> Kx = K(X)  # The kernel map.
>>> np.allclose(Gram * C, Kx(X) * C)

True

Attributes:	n : {Int} Number of samples. d : {Int} Number of features. X : {array-like, sparse matrix}, shape = [n_samples, n_features] Support samples. Gs : {array-like, sparse matrix}, shape = [n, n] Gram matrix associated with the scalar kernel.

Methods

`Gram_dense`(X)	Return the dense Gram matrix associated with the data Y.
`__call__`(Y)	Return the Gram matrix associated with the data Y as a linear operator.
`get_kernel_map`(X)	Return the kernel map associated with the data X.

Gram_dense(X)[source]¶

Return the dense Gram matrix associated with the data Y.

$K(X, Y)$

Parameters:	Y : {array-like, sparse matrix}, shape = [n_samples1, n_features] Samples.
Returns:	K(X, Y) : {array-like} Returns K(X, Y).

T¶: Transposition.

__call__(Y)[source]¶

Return the Gram matrix associated with the data Y as a linear operator.

$K(X, Y)$

Parameters:	Y : {array-like, sparse matrix}, shape = [n_samples1, n_features] Samples.
Returns:	K(X, Y) : LinearOperator Returns K(X, Y).

__init__(X, mu, p)[source]¶

Initialize the DotProduct Operator-Valued Kernel.

Parameters:	X: {array-like, sparse matrix}, shape = [n_samples1, n_features] Support samples. mu : {float}, between 0. and 1. Linear operator acting on the outputs p : {integer} Dimension of the output

__mul__(Ky)[source]¶

Syntaxic sugar.

If Kx is a compatible DotProduct kernel, returns

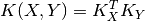
$K(X, Y) = K_X^T K_Y$

Parameters:	Ky : {DotProductKernelMap} Compatible kernel Map (e.g. same kernel but different support data X).
Returns:	K(X, Y) : LinearOperator Returns K(X, Y).

Examples

>>> import operalib as ovk
>>> import numpy as np
>>> X = np.random.randn(100, 10)
>>> K = ovk.DotProductKernel(mu=0.2, p=5)
>>> Gram = K(X, X)
>>> Gram

<500x500 _CustomLinearOperator with dtype=float64>
>>> C = np.random.randn(Gram.shape[0])
>>> Kx = K(X)  # The kernel map.
>>> Ky = K(X)
>>> np.allclose(Gram * C, (Kx.T * Ky) * C)

True

class operalib.kernel_maps.RBFCurlFreeKernelMap(X, gamma)[source]¶

Curl-free RBF Operator-Valued Kernel map of the form:

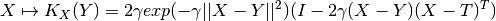
$X \mapsto K_X(Y) = 2\gamma exp(-\gamma||X-Y||^2)(I-2\gamma(X-Y)(X-T)^T)$

This class just fixes the support data X to the kernel. Hence it naturally inherit from RBFCurlFreeKernel

See also

RBFCurlFreeKernel: Curl-free Kernel

Examples

>>> import operalib as ovk
>>> import numpy as np
>>> X = np.random.randn(100, 10)
>>> K = ovk.RBFCurlFreeKernel(1.)
>>> Gram = K(X, X)
>>> Gram

<1000x1000 _CustomLinearOperator with dtype=float64>
>>> C = np.random.randn(Gram.shape[0])
>>> Kx = K(X)  # The kernel map.
>>> np.allclose(Gram * C, Kx(X) * C)

True

Attributes:	n : {Int} Number of samples. d : {Int} Number of features. X : {array-like, sparse matrix}, shape = [n_samples, n_features] Support samples. Gs : {array-like, sparse matrix}, shape = [n, n] Gram matrix.

Methods

`Gram_dense`(X)	Return the dense Gram matrix associated with the data Y.
`__call__`(Y)	Return the Gram matrix associated with the data Y as a linear operator.
`get_kernel_map`(X)	Return the kernel map associated with the data X.
`get_orff_map`(X[, D, random_state])	Return the Random Fourier Feature map associated with the data X.

Gram_dense(X)[source]¶

Return the dense Gram matrix associated with the data Y.

$K(X, Y)$

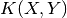
Parameters:	Y : {array-like, sparse matrix}, shape = [n_samples1, n_features] Samples.
Returns:	K(X, Y) : {array-like} Returns K(X, Y).

T¶: Transposition.

__call__(Y)[source]¶

Return the Gram matrix associated with the data Y as a linear operator.

$K(X, Y)$

Parameters:	Y : {array-like, sparse matrix}, shape = [n_samples1, n_features] Samples.
Returns:	K(X, Y) : LinearOperator Returns K(X, Y).

__init__(X, gamma)[source]¶

Initialize the Decomposable Operator-Valued Kernel.

Parameters:	X: {array-like, sparse matrix}, shape = [n_samples1, n_features] Support samples. gamma : {float}, shape = [n_targets, n_targets] RBF kernel parameter.

class operalib.kernel_maps.RBFDivFreeKernelMap(X, gamma)[source]¶

Divergence-free Operator-Valued Kernel of the form:

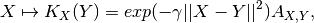
$X \mapsto K_X(Y) = exp(-\gamma||X-Y||^2)A_{X,Y},$

where,

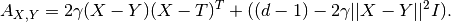
$A_{X,Y} = 2\gamma(X-Y)(X-T)^T+((d-1)-2\gamma||X-Y||^2 I).$

This class just fixes the support data X to the kernel. Hence it naturally inherit from RBFCurlFreeKernel

See also

RBFDivFreeKernel: Divergence-free Kernel

Examples

>>> import operalib as ovk
>>> import numpy as np
>>> X = np.random.randn(100, 10)
>>> K = ovk.RBFDivFreeKernel(1.)
>>> Gram = K(X, X)
>>> Gram

<1000x1000 _CustomLinearOperator with dtype=float64>
>>> C = np.random.randn(Gram.shape[0])
>>> Kx = K(X)  # The kernel map.
>>> np.allclose(Gram * C, Kx(X) * C)

True

Attributes:	n : {Int} Number of samples. d : {Int} Number of features. X : {array-like, sparse matrix}, shape = [n_samples, n_features] Support samples. Gs : {array-like, sparse matrix}, shape = [n, n] Gram matrix.

Methods

`Gram_dense`(X)	Return the dense Gram matrix associated with the data Y.
`__call__`(Y)	Return the Gram matrix associated with the data Y as a linear operator.
`get_kernel_map`(X)	Return the kernel map associated with the data X.
`get_orff_map`(X[, D, random_state])	Return the Random Fourier Feature map associated with the data X.

Gram_dense(X)[source]¶

Return the dense Gram matrix associated with the data Y.

$K(X, Y)$

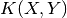
Parameters:	Y : {array-like, sparse matrix}, shape = [n_samples1, n_features] Samples.
Returns:	K(X, Y) : {array-like} Returns K(X, Y).

T¶: Transposition.

__call__(Y)[source]¶

Return the Gram matrix associated with the data Y as a linear operator.

$K(X, Y)$

Parameters:	Y : {array-like, sparse matrix}, shape = [n_samples1, n_features] Samples.
Returns:	K(X, Y) : LinearOperator Returns K(X, Y).

__init__(X, gamma)[source]¶

Initialize the Decomposable Operator-Valued Kernel.

Parameters:	X: {array-like, sparse matrix}, shape = [n_samples1, n_features] Support samples. gamma : {float}, shape = [n_targets, n_targets] RBF kernel parameter.